sfsmooth, one of the most useful Madagascar programs, implements smoothing by triangle filtering.
The idea of triangle filtering is explained in Jon Claerbout’s books Processing versus Inversion and Image Estimation by Example. You can find the explanation in the chapter Smoothing with box and triangle. The triangle filter of radius is a correlation of two box filters. In the Z-transform notation,
$$T_k(Z) = B_k(1/Z)\,B_k(Z)$$
where
$$B_k(Z) = \displaystyle \frac{1}{k}\,\left(1+Z+Z^2+\cdots+Z^k\right) = \frac{1}{k}\,\frac{1-Z^{k+1}}{1-Z}$$
and $k$ is the smoothing radius. Triangle filtering is a very efficient operation, because it requires only $N$ multiplications for the input of size $N$.
Triangle filtering serves as a good approximation to more expensive Gaussian filtering. Repeated triangle filtering rapidly approaches Gaussian filtering (a consequence of the central limit theorem). The following example from jsg/shape/smoo demonstrates how repeated application of triangle smoothing turns a triangle filter into a Gaussian filter

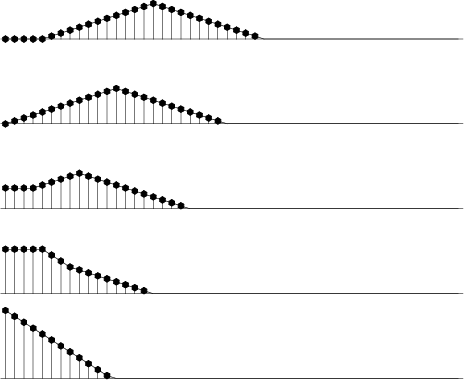
The following example from gee/ajt/triangle demonstrated how sfsmooth handles boundary conditions: the energy is reflected from the side in order to preserve the zero-frequency (DC) component of the input signal. Repeated smoothing or smoothing with a very large radius turns every signal into a constant.
In multiple dimensions, triangle smoothing is applied sequentially in different directions, possible with different radii (controlled by rect#= ) parameter. The following example from gee/ajt/mound shows shapes created by 2-D triangle smoothing after one pass and two passes (repeat=2).


Triangle smoothing is theoretically a self-adjoint operator. Numerically, the adjoint and forward operators are different. The action is controlled by the adj= parameter.
For smoothing with a box instead of a triangle, use sfboxsmooth.
For a different approach to smoothing, try sfgaussmooth, which implements smoothing by recursive Gaussian filtering.
