Acoustic wave equation

Next: Elastic wave equation Up: Basic wave equation Previous: Basic wave equation

Acoustic wave equation

Acoustics is a special case of fluid dynamics (sound waves in gases and liquids) and linear elastodynamics. Note that elastodynamics is a more accurate representation of earth dynamics, but most industrial seismic processing based on acoustic model. Recent interest in quasiacoustic anisotropic approximations to elastic P-waves.

Assume $\tilde{S}(\textbf{x},t;\textbf{x}_s)$ is differentiable constitutive law w.r.t. time . Substituting Eq. (2) into the differentiation of Eq. (1) gives

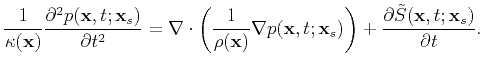$\displaystyle \frac{1}{\kappa(\textbf{x})}\frac{\partial^2 p(\textbf{x},t;\text... ...x}_s)\right) +\frac{\partial \tilde{S}(\textbf{x},t;\textbf{x}_s)}{\partial t}.$

(3)

We introduce $v(\textbf{x})=\sqrt{\kappa(\textbf{x})/\rho(\textbf{x})}$ (compressional p-wave velocity):

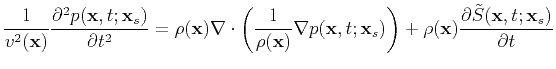$\displaystyle \frac{1}{v^2(\textbf{x})}\frac{\partial^2 p(\textbf{x},t;\textbf{... ...\rho(\textbf{x})\frac{\partial\tilde{S}(\textbf{x},t;\textbf{x}_s)}{\partial t}$

(4)

Under constant density condition, we obtain the 2nd-order equation

$\displaystyle \frac{1}{v^2(\textbf{x})}\frac{\partial^2 p(\textbf{x},t;\textbf{... ...rtial t^2}=\nabla^2 p(\textbf{x},t;\textbf{x}_s)+f_s(\textbf{x},t;\textbf{x}_s)$

(5)

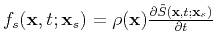where $\nabla^2=\nabla\cdot\nabla=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial z^2}$ , $f_s(\textbf{x},t;\textbf{x}_s)=\rho(\textbf{x})\frac{\partial\tilde{S}(\textbf{x},t;\textbf{x}_s)}{\partial t}$ . In 2D case, it is

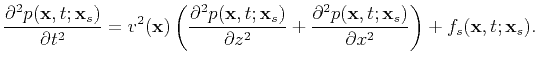$\displaystyle \frac{\partial^2 p(\textbf{x},t;\textbf{x}_s)}{\partial t^2} =v^2... ...textbf{x},t;\textbf{x}_s)}{\partial x^2}\right)+f_s(\textbf{x},t;\textbf{x}_s).$

(6)

A shot of acoustic wavefield obtained at t=0.35s with 4-th order finite difference scheme and the sponge absorbing boundary condition is shown in Figure 1, where the source is put at the center of the model. For 3D, it becomes

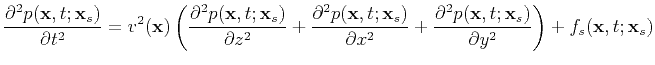$\displaystyle \frac{\partial^2 p(\textbf{x},t;\textbf{x}_s)}{\partial t^2} =v^2... ...\textbf{x},t;\textbf{x}_s)}{\partial y^2}\right)+f_s(\textbf{x},t;\textbf{x}_s)$

(7)

Similarly, we put the source at the center of a 3D volume (size=100x100x100), performed the modeling for 300 steps in time and recorded the corresponding wavefield at kt=250, see Figure 2.


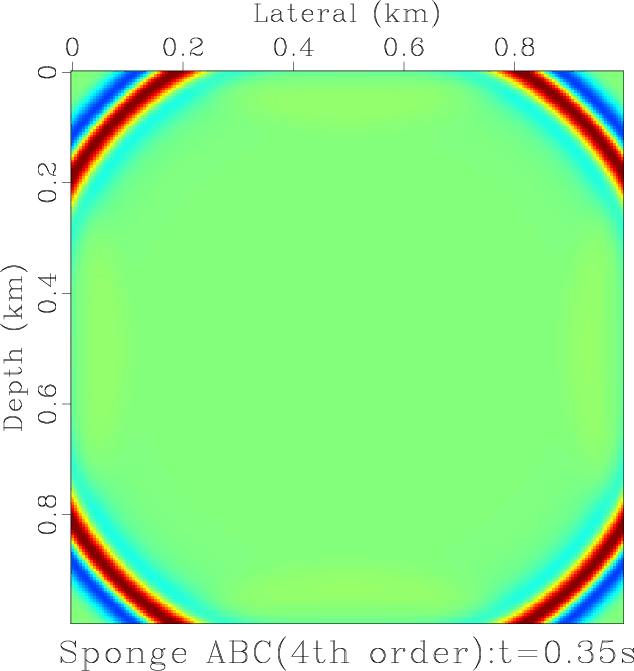
snapfd2d Figure 1. A snap of acoustic wavefield obtained at t=0.35s with 4-th order finite difference scheme and the sponge absorbing boundary condition.


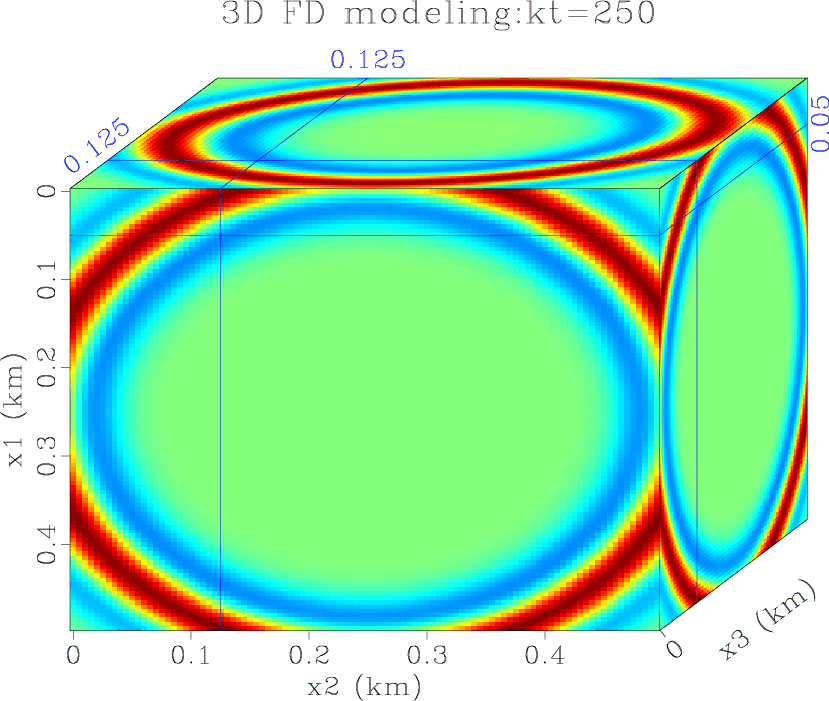
snapfd3d Figure 2. A wavefield snap recorded at kt=250, 300 steps modeled.

The above spatial operator is spatially homogeneous. This isotropic formula is simple and easy to understand, and becomes the basis for many complicated generalizations in which the anisotropy may come in. In 2D case, the elliptically-anisotropic wave equation reads

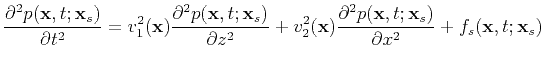$\displaystyle \frac{\partial^2 p(\textbf{x},t;\textbf{x}_s)}{\partial t^2} =v_1... ...al^2 p(\textbf{x},t;\textbf{x}_s)}{\partial x^2}+f_s(\textbf{x},t;\textbf{x}_s)$

(8)

Here, I use the Hess VTI model shown in Figure 3a and Figure 3b. We perform 1000 steps of modeling with time interval $\Delta t=0.001s$ , and capture the wavefield at

, as shown in Figure 4.


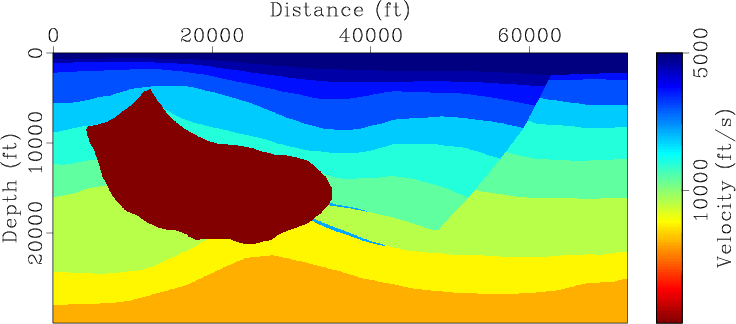
vp,vx Figure 3. Two velocity components of Hess VTI model


snapaniso Figure 4. Wavefield at , 1000 steps of modeling with time interval $\Delta t=0.001s$ performed.

Next: Elastic wave equation Up: Basic wave equation Previous: Basic wave equation

2021-08-31