Understanding iterative thresholding as shaping regularization

Next: MCA using sparsity-promoting shaping Up: MCA with scale-dependent shaping Previous: Analysis-based iterative thresholding

Understanding iterative thresholding as shaping regularization

Note that at each iteration soft thresholding is the only nonlinear operation corresponding to the 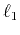$\ell_1$ constraint for the model 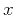, i.e., 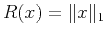$R(x)=\Vert x\Vert _1$ . Shaping regularization (Fomel, 2007,2008) provides a general and flexible framework for inversion without the need for a specific penalty function 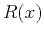when a particular kind of shaping operator is used. The iterative shaping process can be expressed as

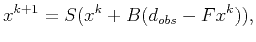$\displaystyle x^{k+1}=S(x^{k}+B(d_{obs}-Fx^{k})),$

(9)

where the shaping operator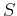

can be a smoothing operator (Fomel, 2007), or a more general operator even a nonlinear sparsity-promoting shrinkage/thresholding operator (Fomel, 2008). It can be thought of a type of Landweber iteration followed by projection, which is conducted via the shaping operator

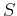. Instead of finding the formula of gradient with a known regularization penalty, we have to focus on the design of shaping operator in shaping regularization. In gradient-based Landweber iteration the backward operator

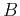is required to be the adjoint of the forward mapping

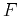, i.e.,

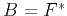; in shaping regularization however, it is not necessarily required. Shaping regularization gives us more freedom to choose a form of

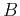to approximate the inverse of

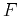so that shaping regularization enjoys faster convergence rate in practice. In the language of shaping regularization, the updating rule in Eq. (7) becomes

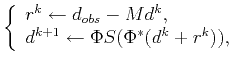$\displaystyle \left\{ \begin{array}{l} r^{k}\leftarrow d_{obs}-Md^{k}, \\ d^{k+1}\leftarrow \Phi S(\Phi^{*}(d^{k}+r^{k})), \end{array} \right.$

(10)

where the backward operator is chosen to be the inverse of the forward mapping.

Next: MCA using sparsity-promoting shaping Up: MCA with scale-dependent shaping Previous: Analysis-based iterative thresholding

2021-08-31