Direction-dependent absorbing boundary conditions

Next: Lowrank approximation Up: Theory Previous: Higher-order terms from the

Direction-dependent absorbing boundary conditions

We propose another innovation using the one-step scheme by incorporating propagation-direction-dependent absorbing boundary conditions into the extrapolation operator. In absorbing boundary layers, we propose to modify the operator

$\displaystyle W(\mathbf{x},\mathbf{k}) = e^{i \left[\phi(\mathbf{x},\mathbf{k},\Delta t)-\mathbf{k} \cdot \mathbf{x}\right]}$

(25)

into the following form:

$\displaystyle W(\mathbf{x},\mathbf{k})_{abc} = e^{i \left[\phi(\mathbf{x},\mat... ...pha (\mathbf{x}-\mathbf{x_t}) \cdot \mathbf{k}}{\vert\mathbf{k}\vert}]^2 } \; ,$

(26)

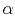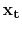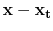where $\alpha$ is the decay parameter and $\mathbf{x_t}$ is the location of the nearest absorbing boundary. The added term $e^{-[\frac{\alpha (\mathbf{x}-\mathbf{x_t}) \cdot \mathbf{k}}{\vert\mathbf{k}\vert}]^2}$ causes exponential decay of the wavefield between the absorbing boundary and the computational boundary (domain truncation), which also depends on the wave traveling direction. 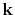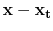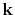When the wave travels normal to the boundary, it will have the maximum absorbing effect because $\mathbf{x}-\mathbf{x_t}$ is in the direction of $\mathbf{k}$ ; on the other hand, there will be no damping when the wave is traveling parallel to the boundary, as the angle between $\mathbf{x}-\mathbf{x_t}$ and $\mathbf{k}$ would be zero. Allowing waves to propagate within the absorbing zone can mitigate artificial reflections from the absorbing boundary, especially at grazing incident angles. The decay term should be applied on both the real wavefield and its first-order time derivative (the imaginary part of the analytical wavefield). This is analogous to the tapering technique described by Cerjan et al. (1985). The absorbing term in the phase function can be physically interpreted as an anisotropic attenuation effect.

The proposed direction-dependent absorbing boundary conditions could also be incorporated into two-step based wave extrapolation methods (Fomel et al., 2013; Song et al., 2013; Fang et al., 2014) using lowrank approximation, by separately applying the damping operator on both the wavefield and its time derivative. However, since two-step schemes do not allow a direct incorporation of the absorbing boundary condition into the wave propagation matrix, additional Fourier transforms will be required. The one-step implementation is more computationally efficient and straightforward.

Next: Lowrank approximation Up: Theory Previous: Higher-order terms from the

2016-11-16