 |
 |
 |
 | Applications of plane-wave destruction filters |  |
![[pdf]](icons/pdf.png) |
Next: Acknowledgments
Up: Fomel: Plane-wave destructors
Previous: Signal and noise separation
Plane-wave destruction filters with an improved finite-difference
design can be a valuable tool in processing multidimensional seismic
data. On several examples, I showed their good performance in such
problems as fault detection, missing data interpolation, and noise
attenuation. Although only 2-D examples were demonstrated, it
is straightforward to extend the method to 3-D applications by
considering two orthogonal plane-wave slopes.
The similarities
and differences between plane-wave destructors and 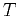 -
-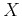 prediction-error filters can be summarized as follows:
prediction-error filters can be summarized as follows:
Similarities:
- Both types of filters operate in the original time-and-space
domain of recorded data.
- Both filters aim to predict local plane-wave events in the data.
- In most problems, one filter type can be replaced by the other,
and certain techniques, such as Claerbout's trace interpolation
method, are common for both approaches.
Differences:
- The design of plane-wave destructors is purely deterministic and
follows the plane-wave differential equation. The design of
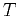 -
-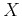 PEF has statistical roots in the framework of the maximum-entropy
spectral analysis (Burg, 1975). In principle,
PEF has statistical roots in the framework of the maximum-entropy
spectral analysis (Burg, 1975). In principle, 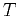 -
-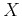 PEF
can characterize more complex signals than local plane waves.
PEF
can characterize more complex signals than local plane waves.
- In the case of PEF, we estimate filter coefficients. In the
case of plane-wave destructors, the estimated quantity is the local
plane-wave slope. Several important distinctions follow from that
difference:
- The filter-estimation problem is linear. The slope estimation
problem, in the case of the improved filter design, is non-linear,
but allows for an iterative linearization. In general, non-linearity
is an undesirable feature because of local minima and the dependence
on initial conditions. However, we can sometimes use it creatively.
For example, it helped to avoid aliased dips in the trace
interpolation example.
- Non-stationarity is handled gracefully in the local slope
estimation. No local windows are required to produce a smoothly
varying estimate of the local slope. This is a much more difficult
issue for PEFs because of the largely under-determined problem.
- Local slope has a clearly interpretable physical meaning, which
allows for easy quality control of the results. The coefficients
of
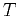 -
-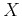 PEFs are much more difficult to interpret.
PEFs are much more difficult to interpret.
- The efficiency of the two approaches is difficult to compare.
Plane-wave destructors are generally more efficient to apply because
of the small number of filter coefficients. However, they
may require more computation at the estimation stage because of the
non-linearity problem.
 |
 |
 |
 | Applications of plane-wave destruction filters |  |
![[pdf]](icons/pdf.png) |
Next: Acknowledgments
Up: Fomel: Plane-wave destructors
Previous: Signal and noise separation
2014-03-29
![]() -
-![]() prediction-error filters can be summarized as follows:
prediction-error filters can be summarized as follows: