Applications of plane-wave destruction filters

Fault detection

The use of prediction-error filters in the problem of detecting local discontinuities was suggested by Claerbout (1999,1994), and further refined by Schwab et al. (1996) and Schwab (1998). Bednar (1998) used simple plane-destruction filters in a similar setting to compute coherency attributes.

To test the performance of the improved plane-wave destructors, I chose several examples from Claerbout (1999). Figure 2 introduces the first example. The left plot of the figure shows a synthetic model, which resembles sedimentary layers with a plane unconformity and a curvilinear fault. The model contains 200 traces of 200 samples each. The right plot shows the corresponding texture (Claerbout and Brown, 1999), obtained by convolving a field of random numbers with the inverse of plane-wave destruction filters. The inverses are constructed using helical filtering techniques (Fomel, 2001; Claerbout, 1998). Texture plots allow us to quickly access the ability of the destruction filters to characterize the main locally plane features in the data. The dip field was estimated by the linearization method of the previous section. 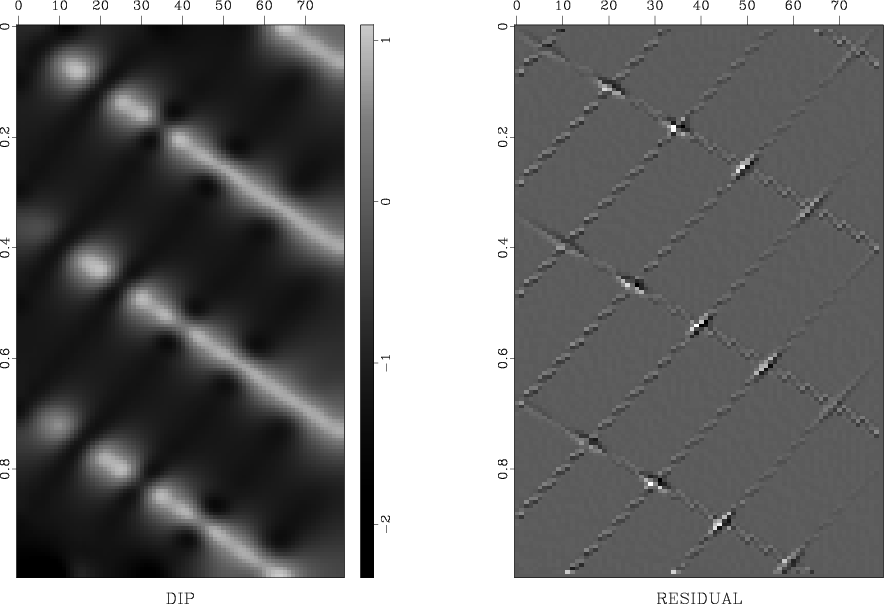The dip field itself and the prediction residual [the left-hand side of equation (13)] are shown in the left and right plots of Figure 3 respectively. We observe that the texture plot does reflect the dip structure of the input data, which indicates that the dip field was estimated correctly. The fault and unconformity are clearly visible both in the dip estimate and in the residual plots. Anywhere outside the slope discontinuities and the boundaries, the residual is close to zero. Therefore, it can be used directly as a fault detection measure. Comparing the residual plot in Figure 3 with the analogous plot of Claerbout (1999,1994), reproduced in Figure 4, establishes a superior performance of the improved finite-difference destructors in comparison with that of the local $T$-$X$ prediction-error filters.

sigmoid-txr
Figure 2. Synthetic sedimentary model. Left plot: Input data. Right plot: Its texture. The texture is computed by convolving a field number with the inverse of plane-wave destruction filters. It highlights the position of estimated local plane waves.

sigmoid-dip
Figure 3. Synthetic sedimentary model. Left plot: Estimated dip field. Right plot: Prediction residual. Large absolute residual indicates the location of faults.

sigmoid-clae Figure 4. Prediction residual of the 11-point prediction-error filter estimated in local 20x6 windows (reproduced from (Claerbout, 1999)).To be compared with the right plot in Figure 3.

The left plot in Figure 5 introduces a simpler synthetic test. The model is composed of linear events with two conflicting slopes. A regularized dip field estimation attempts to smooth the estimated dip in the places where it is not constrained by the data (the left plot of Figure 6.) The effect of smoothing is clearly seen in the texture image (the right plot in Figure 5). The corresponding residual (the right plot of Figure 6) shows suppressed linear events and highlights the places of their intersection. Residuals are large at intersections because a single dominant dip model fails to adequately represent both conflicting dips.

conflict-txr
Figure 5. Conflicting dips synthetic. Left plot: Input data. Right plot: Its texture.

conflict-dip
Figure 6. Conflicting dips synthetic. Left plot: Estimated dip field. Right plot: Prediction residual.Large absolute residual indicates the location of conflicting dips.

The left plot in Figure 7 shows a real shot gather: a portion of Yilmaz and Cumro (1983) data set 27. The initial dip in the dip estimation program was set to zero. Therefore, the texture image (the right plot in Figure 7) contains zero-dipping plane waves in the places of no data. Everywhere else the dip is accurately estimated from the data. The data contain a missing trace at about 0.7 km offset and a slightly shifted (possibly mispositioned) trace at about 1.1 km offset. The mispositioned trace is clearly visible in the dip estimate (the left plot in Figure 8), and the missing trace is emphasized in the residual image (the right plot in Figure 8). Additionally, the residual image reveals the forward and back-scattered surface waves, hidden under more energetic reflections in the input data.

yc27-txr
Figure 7. Real shot gather. Left plot: Input data. Right plot: Its texture.

yc27-dip
Figure 8. Real shot gather. Left plot: Estimated dip field. Right plot: Prediction residual. The residual highlights surface waves hidden under dominant reflection events in the original data.

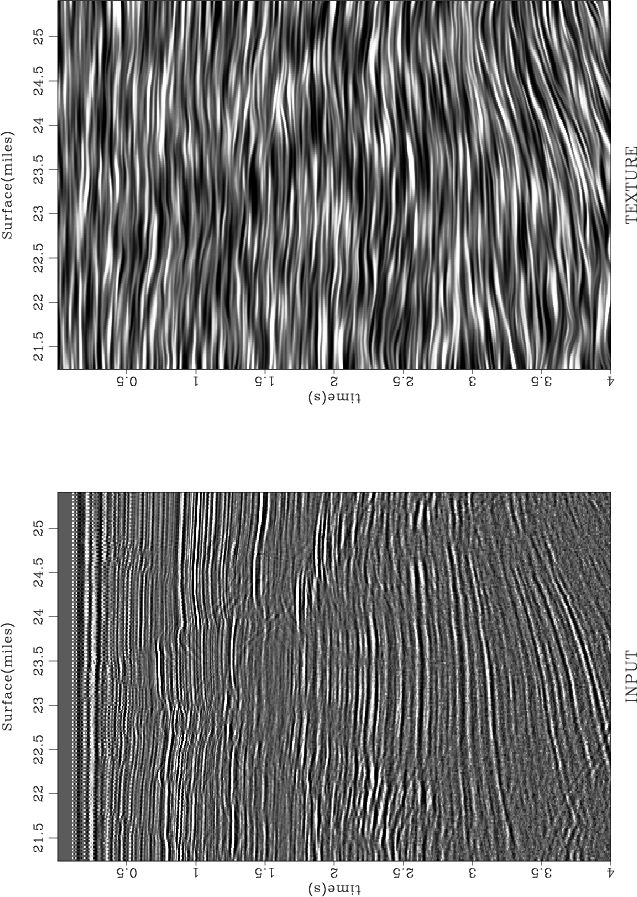
Figure 9 shows a stacked time section from the Gulf of Mexico and its corresponding texture. The texture plot demonstrates that the estimated dip (the left plot of Figure 10) reflects the dominant local dip in the data. After the plane waves with the dominant dip are removed, many hidden diffractions appear in the residual image (the right plot in Figure 10.) The enhanced diffraction events can be used, for example, for estimating the medium velocity (Harlan et al., 1984).

dgulf-txr
Figure 9. Time section from the Gulf of Mexico. Left plot: Input data. Right plot: Its texture. The texture plot shows dominant local dips estimated from the data.

dgulf-dip
Figure 10. Time section from the Gulf of Mexico. Left plot: Estimated dip field. Right plot: Prediction residual.The residual highlights diffraction events hidden under dominant reflections in the original data.

Overall, the examples of this subsection show that the finite-difference plane-wave destructors provide a reliable tool for enhancement of discontinuities and conflicting slopes in seismic images. The estimation step of the fault detection procedure produces an image of the local dominant dip field, which may have its own interpretational value. An extension to 3-D is possible, as outlined by Schwab (1998), Clapp (2001), and Fomel (2001).

Applications of plane-wave destruction filters