 |
 |
 |
 | Madagascar Programming Reference Manual |  |
 |
![[pdf]](icons/pdf.png) |
 |
Next: Products of operators
Up: Introduction
Previous: Introduction
Mathematically speaking an operator is a function of a function, i.e. a rule (or mapping) according to which a function 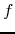 is transformed into another function
is transformed into another function 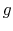 . We use the notation
. We use the notation ![$ g=R[f]$](img187.png) or simply
or simply 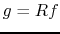 , where
, where 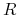 denotes the operator. Examples of operators are the derivative, the integral, convolution (with a specific function), multiplication by a scalar and others. Note that in general the domains of
denotes the operator. Examples of operators are the derivative, the integral, convolution (with a specific function), multiplication by a scalar and others. Note that in general the domains of 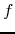 and
and 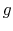 are not necessarily the same. For example, in the case of the derivative, the domain of
are not necessarily the same. For example, in the case of the derivative, the domain of 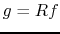 is the subset of the domain of
is the subset of the domain of 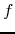 , in which
, in which 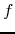 is smooth. In particular if
is smooth. In particular if 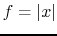 ,
,
![$ x\in[-1,1]$](img191.png) , then the domain of
, then the domain of 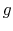 is
is
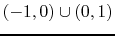 .
.
An important class of operators are the linear operators. An operator 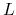 is linear if for any two functions
is linear if for any two functions 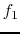 ,
, 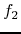 and any two scalars
and any two scalars 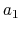 ,
, 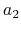 ,
,
![$ L[a_1f_1+a_1f_2]=a_1Lf_1 + a_2Lf_2$](img198.png) . The derivative, integral, convolution and multiplication by scalar are all linear operators.
. The derivative, integral, convolution and multiplication by scalar are all linear operators.
In the discrete world, operators act on vectors and linear operators are in fact matrices, with which the vectors are multiplied. (Multiplication by a matrix is a linear operation, since
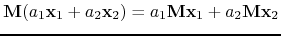 ). In fact many of the calculations performed routinely in science and engineering are essentially matrix multiplications in disguise. For example assume a vector
). In fact many of the calculations performed routinely in science and engineering are essentially matrix multiplications in disguise. For example assume a vector
![$ \mathbf{x}=[x_1\;x_2\;\ldots\;x_n]^T$](img200.png) with length
with length 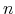 (superscript
(superscript 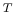 denotes transpose). Padding this vector with
denotes transpose). Padding this vector with 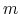 zeros, produces another vector
zeros, produces another vector
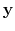 with
with
Note that as in the case of functions, the domains of
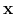 and
and
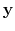 are different:
are different:
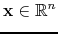 (or more generally
(or more generally
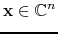 ), while
), while
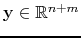 (or
(or
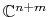 ).
).
Similarly, one can define convolution of
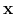 with
with
![$ \mathbf{a}=[a_1\;a_2\;\dots\;a_m]^T$](img217.png) as the multiplication of
as the multiplication of
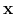 with
with
and many other operations as matrix multiplications. Other operators are the identity operator is the identity matrix
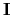 and is implemented by [sec:copy]copy.c and [sec:ccopy]ccopy.c and the null operator (or zero matrix
and is implemented by [sec:copy]copy.c and [sec:ccopy]ccopy.c and the null operator (or zero matrix
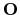 ), which is implemented by [sec:adjnull]adjnull.c. For the rest of this introduction, the boldface notation will imply specifically discrete operators, while the normal fonts will imply operators on either continuous or discrete mathematical entities.
), which is implemented by [sec:adjnull]adjnull.c. For the rest of this introduction, the boldface notation will imply specifically discrete operators, while the normal fonts will imply operators on either continuous or discrete mathematical entities.
 |
 |
 |
 | Madagascar Programming Reference Manual |  |
 |
![[pdf]](icons/pdf.png) |
 |
Next: Products of operators
Up: Introduction
Previous: Introduction
2011-07-02
![]() is linear if for any two functions
is linear if for any two functions ![]() ,
, ![]() and any two scalars
and any two scalars ![]() ,
, ![]() ,
,
![]() . The derivative, integral, convolution and multiplication by scalar are all linear operators.
. The derivative, integral, convolution and multiplication by scalar are all linear operators.
![]() ). In fact many of the calculations performed routinely in science and engineering are essentially matrix multiplications in disguise. For example assume a vector
). In fact many of the calculations performed routinely in science and engineering are essentially matrix multiplications in disguise. For example assume a vector
![]() with length
with length ![]() (superscript
(superscript ![]() denotes transpose). Padding this vector with
denotes transpose). Padding this vector with ![]() zeros, produces another vector
zeros, produces another vector
![]() with
with
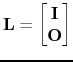 , where
, where
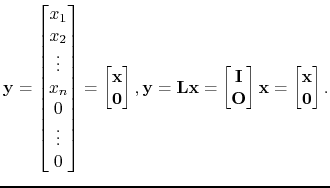
![]() with
with
![]() as the multiplication of
as the multiplication of
![]() with
with
