Next: Appendix D: REFLECTION FROM Up: Fomel & Stovas: Generalized Previous: Appendix B: LINEAR SLOTH

Appendix C: REFLECTION FROM A HYPERBOLIC REFLECTOR IN A HOMOGENEOUS VELOCITY MODEL

In this appendix, we derive an analytical expression for reflection traveltime from a hyperbolic reflector in a homogeneous velocity model (Figure C-1). Similar derivations apply to an elliptic reflector and were used previously in the theory of dip moveout, offset continuation, and non-hyperbolic common-reflection surface (Fomel and Kazinnik, 2009; Stovas and Fomel, 1996; Fomel, 2003).


hyper Figure 9. Reflection from a hyperbolic reflector in a homogeneous velocity model (a scheme).

Consider the source point and the receiver point at the surface above a 2-D constant-velocity medium and a hyperbolic reflector defined by the equation

$\begin{displaymath} z(x) = \sqrt{h^2 + x^2\,\tan^2{\alpha}}\;. \end{displaymath}$

(54)

The reflection traveltime as a function of the reflection point location

$\begin{displaymath} t = \frac{\sqrt{(x_s-y)^2 + z^2(y)} + \sqrt{(x_r-y)^2+z^2(y)}}{V}\;. \end{displaymath}$

(55)

According to Fermat's principle, the traveltime should be stationary with respect to the reflection point

$\begin{displaymath} 0 = \frac{\partial t}{\partial y} = \frac{y-x_s + y\,\tan^2{... ...2{\alpha}}{V\,\sqrt{(x_r-y)^2 + h^2 + y^2\,\tan^2{\alpha}}}\;. \end{displaymath}$

(56)

Putting two terms in equation C-3 on different sides of the equation, squaring them, and reducing their difference to a common denominator, we arrive at the equation

$\displaystyle 0$	$\textstyle =$	$\displaystyle \left[\frac{y}{\cos^2{\alpha}} - x_s\right]^2\,\left[(x_r-y)^2 + h^2 + y^2\,\tan^2{\alpha}\right]$
	$\textstyle -$	$\displaystyle \left[\frac{y}{\cos^2{\alpha}} - x_r\right]^2\,\left[(x_s-y)^2 + h^2 + y^2\,\tan^2{\alpha}\right]$	(57)

which simplifies to the following quadratic equation with respect to

$\begin{displaymath} y^2\,(x_s+x_r)\,\tan^2{\alpha} - 2\,y\,\left(x_s\,x_r\,\s... ...{\alpha} - h^2\right) - h^2\,(x_s+x_r)\,\cos^2{\alpha} = 0\;. \end{displaymath}$

(58)

The discriminant is

$\begin{displaymath} D = \left(x_s\,x_r\,\sin^2{\alpha}-h^2\right)^2 + h^2\,(x... ... = (h^2+x_s^2\,\sin^2{\alpha})\,(h^2+x_r^2\,\sin^2{\alpha})\;. \end{displaymath}$

(59)

Only one of the two branches of the solution

$\displaystyle y$	$\textstyle =$	$\displaystyle \frac{x_s\,x_r\,\sin^2{\alpha}-h^2 + \sqrt{(h^2+x_s^2\,\sin^2{\alpha})\,(h^2+x_r^2\,\sin^2{\alpha})}}{(x_s+x_r)\,\tan^2{\alpha}}$
	$\textstyle =$	$\displaystyle \frac{h^2\,(x_s+x_r)\,\cos^2{\alpha}}{h^2 - x_s\,x_r\,\sin^2{\alpha} + \sqrt{(h^2+x_s^2\,\sin^2{\alpha})\,(h^2+x_r^2\,\sin^2{\alpha})}}$	(60)

has physical meaning. Substituting equation C-7 into equation C-2, we obtain, after a number of algebraic simplifications,

$\begin{displaymath} t = \frac{\sqrt{2 h^2 + x_s^2 + x_r^2 - 2\,x_s\,x_r\,\cos... ...2+x_s^2\,\sin^2{\alpha})\,(h^2+x_r^2\,\sin^2{\alpha})}}}{V}\;. \end{displaymath}$

(61)

Making the variable change in equation C-8 from

and

to the midpoint and offset coordinates

and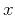

according to

, we notice that this equation is exactly equivalent to equation 1 with the following definition of parameters:

$\displaystyle t_0$	$\textstyle =$	$\displaystyle \frac{2\,\sqrt{h^2 + m^2\,\sin^2{\alpha}}}{V}\;,$	(62)
$\displaystyle a$	$\textstyle =$	$\displaystyle \frac{2-\sin^2{\alpha}}{V^2}\;,$	(63)
$\displaystyle b$	$\textstyle =$	$\displaystyle \frac{\sin^2{\alpha}}{V^2}\,\frac{h^2 - m^2\,\sin^2{\alpha}}{h^2 + m^2\,\sin^2{\alpha}}\;,$	(64)
$\displaystyle c$	$\textstyle =$	$\displaystyle \frac{\sin^4{\alpha}}{V^4}\;,$	(65)
$\displaystyle \xi$	$\textstyle =$	$\displaystyle \frac{1}{2}\;.$	(66)

Next: Appendix D: REFLECTION FROM Up: Fomel & Stovas: Generalized Previous: Appendix B: LINEAR SLOTH

2013-03-02