Next: Predictive painting in 2-D Up: Fomel: Predictive painting Previous: Introduction

Destruction and prediction of plane waves

Plane-wave destruction originates from a local plane-wave model for characterizing seismic data (Fomel, 2002). The mathematical basis is the local plane differential equation

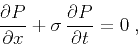$\begin{displaymath} \frac{\partial P}{\partial x} + \sigma\,\frac{\partial P}{\partial t} = 0\;, \end{displaymath}$

(1)

where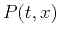

is the wave field and 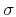$\sigma$ is the local slope, which may also depend on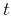

and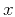

(Claerbout, 1992). In the case of a constant slope, equation 1 has the simple general solution

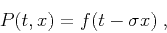$\begin{displaymath} P(t,x) = f(t - \sigma x)\;, \end{displaymath}$

(2)

where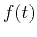

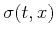is an arbitrary waveform. Equation 2 is nothing more than a mathematical description of a plane wave. Assuming that the slope $\sigma(t,x)$ varies in time and space, one can design a local operator to propagate each trace to its neighbors.

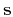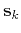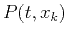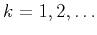Let $\mathbf{s}$ represent a seismic section as a collection of traces: $\mathbf{s} = \left[\mathbf{s}_1 \; \mathbf{s}_2 \; \ldots \; \mathbf{s}_N\right]^T$ , where $\mathbf{s}_k$ corresponds to for $k=1,2,\ldots$ A plane-wave destruction operator (Fomel, 2002) effectively predicts each trace from its neighbor and subtracts the prediction from the original trace. In the linear operator notation, the plane-wave destruction operation can be defined as

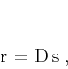$\begin{displaymath} \mathbf{r} = \mathbf{D\,s}\;, \end{displaymath}$

(3)

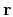where $\mathbf{r}$ is the destruction residual, and 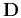$\mathbf{D}$ is the destruction operator defined as

$\begin{displaymath} \mathbf{D} = \left[\begin{array}{ccccc} \mathbf{I} & 0... ...& - \mathbf{P}_{N-1,N} & \mathbf{I} \\ \end{array}\right]\;, \end{displaymath}$

(4)

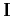where $\mathbf{I}$ stands for the identity operator, and 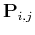$\mathbf{P}_{i,j}$ describes prediction of trace

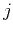from trace

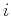. Prediction of a trace consists of shifting the original trace along dominant event slopes. The prediction operator is a numerical solution of equation 1 for local plane wave propagation in the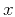

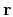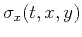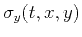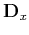direction. The dominant slopes are estimated by minimizing the prediction residual $\mathbf{r}$ using regularized least-squares optimization. I employ shaping regularization (Fomel, 2007a) for controlling the smoothness of the estimated slope fields. 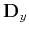In the 3-D case, a pair of inline and crossline slopes, $\sigma_x(t,x,y)$ and $\sigma_y(t,x,y)$ , and a pair of destruction operators, $\mathbf{D}_x$ and $\mathbf{D}_y$ , are required to characterize the 3-D structure. Each prediction in 3-D occurs in either inline or crossline direction and thus conforms to equation 4. However, as explained below in the discussion of Dijkstra's algorithm, it is possible to arrange all 3-D traces in a sequence for further processing.

Prediction of a trace from a distant neighbor can be accomplished by simple recursion. Predicting trace 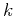from trace 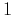is simply

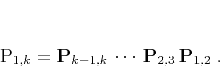$\begin{displaymath} \mathbf{P}_{1,k} = \mathbf{P}_{k-1,k}\, \cdots\,\mathbf{P}_{2,3}\,\mathbf{P}_{1,2}\;. \end{displaymath}$

(5)

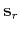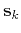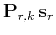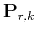If $\mathbf{s}_r$ is a reference trace, then the prediction of trace $\mathbf{s}_k$ is $\mathbf{P}_{r,k}\,\mathbf{s}_r$ . I call the recursive operator $\mathbf{P}_{r,k}$ predictive painting. Once the elementary prediction operators in equation 4 are determined by plane-wave destruction, predictive painting can spread information from a given trace to its neighbors recursively by following the local structure of seismic events. The next section illustrates the painting concept using 2-D examples.

Next: Predictive painting in 2-D Up: Fomel: Predictive painting Previous: Introduction

2013-03-02