 |
 |
 |
 | Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Derivation of the FIR
Up: Appendix A: Hilbert transform
Previous: Appendix A: Hilbert transform
First, to characterize the FIR for signal differentiators, we
transform the Leibniz series
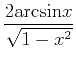 to power series
(Lehmer, 1985)
to power series
(Lehmer, 1985)
![$\displaystyle \frac{2{\rm {arcsin}}x}{\sqrt{1-x^2}}=2x \left[1+\sum_{m=1}^{\infty}\frac{(2{\rm {m}})!!} {(2{\rm {m}}+1)!!}x^{2m}\right].$](img57.png) |
(11) |
We substitute sin
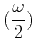 for
for 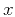 , and after
rearrangement and truncation of the first
, and after
rearrangement and truncation of the first 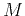 terms, we obtain
terms, we obtain
![\begin{displaymath}\begin{split}& \frac{\omega}{\sqrt{1-{\rm {sin}}^{2}\displays...
...m}+ o((\frac{1-{\rm {cos}}\omega}{2})^{M+1})\right] \end{split}\end{displaymath}](img60.png) |
(12) |
and after manipulation
![\begin{displaymath}\begin{split}\omega & =2{\rm {sin}}\frac{\omega}{2}{\rm {cos}...
...}+ o((\frac{1-{\rm {cos}}\omega}{2})^{M+1})\right]. \end{split}\end{displaymath}](img61.png) |
(13) |
We ignore the higher order terms and we obtain the 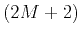 th-order
causal transfer function of the derivative operator as
th-order
causal transfer function of the derivative operator as
![$\displaystyle \hat{F}_{DD}(z)\approx-\frac{1-z^{-2}}{2}\left\{z^{-M}+ \sum_{m=1...
...\rm {m}}+ 1)!!}{\cdot}z^{-(M-m)}\left[-\frac{(1-z^{-1})^2}{4}\right]^m\right\}.$](img63.png) |
(14) |
 |
 |
 |
 | Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation |  |
![[pdf]](icons/pdf.png) |
Next: Derivation of the FIR
Up: Appendix A: Hilbert transform
Previous: Appendix A: Hilbert transform
2015-05-07
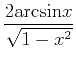 to power series
(Lehmer, 1985)
to power series
(Lehmer, 1985)