Next: Choice of a unitless
Up: PRECONDITIONING THE REGULARIZATION
Previous: Importance of scaling
In the statistical literature is a concept that repeatedly arises,
the idea that some statistical variables are IID, namely Independent, Identically Distributed.
In practice, we see many random-looking variables,
some much closer than others to IID.
Theoretically, the ID part of IID means the random variables come from Identical
probability Density functions.
In practice, the ID part mostly means the variables have the same variance.
The ``I'' before the ID means the variables are statistically Independent of one another.
Neighboring values should not be positively correlated, meaning low frequencies are present.
In the subject area of this book, signals, images, and Earth volumes,
the ``I'' before the ID means our residual spaces are white--have
all frequencies present in roughly equal amounts.
In other words the ``I'' means the statistical variables
have no significant correlation in time or space.
Chapter ![[*]](icons/crossref.png) gives a method of finding a
filter as a model styler (regularizer) that accomplishes this goal.
IID random variables have fairly uniform variance in both physical space and in Fourier space.
gives a method of finding a
filter as a model styler (regularizer) that accomplishes this goal.
IID random variables have fairly uniform variance in both physical space and in Fourier space.
|
IID random variables have uniform variance in both physical space and Fourier space.
|
In a geophysical project,
it is important the residual between observed data and modeled data is not far from IID.
To raw residuals,
we should apply weights and filters to get IID residuals.
We minimize sums of squares of residuals.
If any residuals are small, the squares are tiny,
so such regression equations are effectively ignored.
We would hardly ever want residuals ignored.
Echo seismograms get weak at late time.
So,
even with a bad fit,
the difference between real and theoretical seismograms
is necessarily weak at late times.
We do not want the data at late times to be ignored.
So,
we boost up the residual there.
We choose 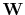 to be a diagonal matrix that boosts late times
in the regression
to be a diagonal matrix that boosts late times
in the regression
 .
.
An example with too much low (spatial) frequency in a residual might arise in a topographic study.
It is not unusual for the topographic wavelength to exceed the survey size.
Here, we should choose 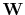 to be a filter to boost up the higher frequencies.
Perhaps,
to be a filter to boost up the higher frequencies.
Perhaps, 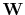 should contain a derivative or a Laplacian.
If you set up and solve a data-modeling problem
and then find
should contain a derivative or a Laplacian.
If you set up and solve a data-modeling problem
and then find 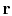 is not IID,
you should consider changing your
is not IID,
you should consider changing your 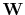 .
Chapter
.
Chapter ![[*]](icons/crossref.png) provides a systematic
approach to whitening residuals.
provides a systematic
approach to whitening residuals.
Now, let us include regularization
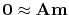 and a preconditioning variable
and a preconditioning variable 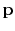 .
We have our data-fitting goal and our model-styling goal;
the first with a residual
.
We have our data-fitting goal and our model-styling goal;
the first with a residual 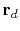 in data space, the second with a residual
in data space, the second with a residual 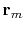 in model space.
We have had to choose a regularization operator
in model space.
We have had to choose a regularization operator
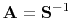 and a scaling factor
and a scaling factor 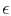 .
.
This system of two regressions could be packed into one;
the two residual vectors stacked on top of each other,
likewise the operators 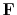 and
and
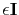 .
The IID notion seems to apply to this unified system
which gives us a clue as to
how we should have chosen the regularization operator
.
The IID notion seems to apply to this unified system
which gives us a clue as to
how we should have chosen the regularization operator 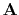 .
Not only should
.
Not only should 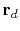 be IID, but also should
be IID, but also should 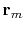 --within a scale
--within a scale 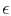 ,
,
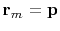 .
Thus, the preconditioning variable is not simply something to speed computational convergence.
It is a variable that should be IID.
If it is not coming out that way, we should consider changing
.
Thus, the preconditioning variable is not simply something to speed computational convergence.
It is a variable that should be IID.
If it is not coming out that way, we should consider changing 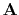 .
Chapter
.
Chapter ![[*]](icons/crossref.png) addresses the task of choosing an
addresses the task of choosing an 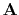 ,
so
,
so 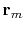 comes out IID.
comes out IID.
We should choose a weighting function (and/or operator) 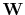 ,
so data residuals are IID.
We should also choose our regularization operator
,
so data residuals are IID.
We should also choose our regularization operator
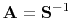 so the preconditioning variable
so the preconditioning variable 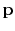 comes out IID.
comes out IID.
|
Next: Choice of a unitless
Up: PRECONDITIONING THE REGULARIZATION
Previous: Importance of scaling
2015-05-07
![]() to be a diagonal matrix that boosts late times
in the regression
to be a diagonal matrix that boosts late times
in the regression
![]() .
.
![]() to be a filter to boost up the higher frequencies.
Perhaps,
to be a filter to boost up the higher frequencies.
Perhaps, ![]() should contain a derivative or a Laplacian.
If you set up and solve a data-modeling problem
and then find
should contain a derivative or a Laplacian.
If you set up and solve a data-modeling problem
and then find ![]() is not IID,
you should consider changing your
is not IID,
you should consider changing your ![]() .
Chapter
.
Chapter ![]() provides a systematic
approach to whitening residuals.
provides a systematic
approach to whitening residuals.
![]() and a preconditioning variable
and a preconditioning variable ![]() .
We have our data-fitting goal and our model-styling goal;
the first with a residual
.
We have our data-fitting goal and our model-styling goal;
the first with a residual ![]() in data space, the second with a residual
in data space, the second with a residual ![]() in model space.
We have had to choose a regularization operator
in model space.
We have had to choose a regularization operator
![]() and a scaling factor
and a scaling factor ![]() .
.