 |
 |
 |
 | Interferometric imaging condition for wave-equation migration |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B
Up: Appendix A
Previous: Appendix A
Consider a medium whose behavior is completely defined by the acoustic
velocity, i.e. assume that the density
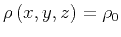 is
constant and the velocity
is
constant and the velocity
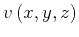 fluctuates around a homogenized
value
fluctuates around a homogenized
value
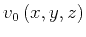 according to the relation
according to the relation
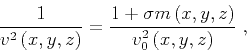 |
(12) |
where the parameter 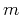 characterizes the type of random fluctuations
present in the velocity model, and
characterizes the type of random fluctuations
present in the velocity model, and 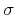 denotes their strength.
denotes their strength.
Consider the covariance orientation vectors
defining a coordinate system of arbitrary orientation in space. Let
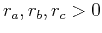 be the covariance range parameters in the
directions of
be the covariance range parameters in the
directions of 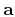 ,
,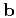 and
and 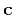 , respectively.
, respectively.
We define a covariance function
![\begin{displaymath}
\mathrm{cov} \left (x,y,z \right)= \exp \left [-l^{\alpha} \left (x,y,z \right)\right]\;,
\end{displaymath}](img80.png) |
(16) |
where
![$\alpha \in [0,2]$](img81.png) is a distribution shape parameter and
is a distribution shape parameter and
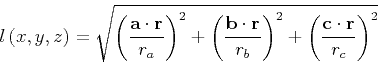 |
(17) |
is the distance from a point at coordinates
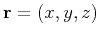 to the
origin in the coordinate system defined by
to the
origin in the coordinate system defined by
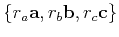 .
.
Given the IID Gaussian noise field
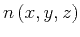 , we obtain the random
noise
, we obtain the random
noise
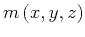 according to the relation
according to the relation
![\begin{displaymath}
m \left (x,y,z \right)=
\mathscr{F}^{-1}
\left [\sqrt{\wideh...
...ight)} \;
\widehat{ n} \left (k_x,k_y,k_z \right)
\right]\;,
\end{displaymath}](img87.png) |
(18) |
where 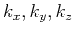 are wavenumbers associated with the spatial
coordinates
are wavenumbers associated with the spatial
coordinates 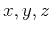 , respectively. Here,
, respectively. Here,
are Fourier transforms of the covariance function 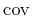 and the noise
and the noise
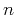 ,
,
![$\mathscr{F}[\cdot]$](img95.png) denotes Fourier transform, and
denotes Fourier transform, and
![$\mathscr{F}^{-1}[\cdot]$](img96.png) denotes inverse Fourier transform. The
parameter
denotes inverse Fourier transform. The
parameter 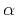 controls the visual pattern of the field, and
controls the visual pattern of the field, and
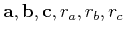 control the size and orientation of a
typical random inhomogeneity.
control the size and orientation of a
typical random inhomogeneity.
 |
 |
 |
 | Interferometric imaging condition for wave-equation migration |  |
![[pdf]](icons/pdf.png) |
Next: Appendix B
Up: Appendix A
Previous: Appendix A
2013-08-29
![]() is
constant and the velocity
is
constant and the velocity
![]() fluctuates around a homogenized
value
fluctuates around a homogenized
value
![]() according to the relation
according to the relation
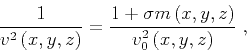
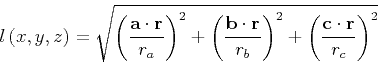
![]() , we obtain the random
noise
, we obtain the random
noise
![]() according to the relation
according to the relation
![\begin{displaymath}
m \left (x,y,z \right)=
\mathscr{F}^{-1}
\left [\sqrt{\wideh...
...ight)} \;
\widehat{ n} \left (k_x,k_y,k_z \right)
\right]\;,
\end{displaymath}](img87.png)