Adjoints of products are reverse-ordered products of adjoints

Next: Nearest-neighbor coordinates Up: FAMILIAR OPERATORS Previous: Zero padding is the

Adjoints of products are reverse-ordered products of adjoints

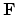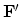Here we examine an example of the general idea that adjoints of products are reverse-ordered products of adjoints. For this example we use the Fourier transformation. No details of Fourier transformation are given here and we merely use it as an example of a square matrix $\bold F$ . We denote the complex-conjugate transpose (or adjoint) matrix with a prime, i.e., $\bold F'$ . The adjoint arises naturally whenever we consider energy. 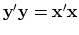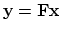The statement that Fourier transforms conserve energy is $\bold y'\bold y=\bold x'\bold x$ where $\bold y= \bold F \bold x$ . 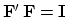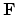Substituting gives $\bold F' \bold F = \bold I$ , which shows that the inverse matrix to Fourier transform happens to be the complex conjugate of the transpose of $\bold F$ .

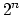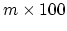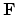With Fourier transforms, zero padding and truncation are especially prevalent. Most subroutines transform a dataset of length of , whereas dataset lengths are often of length $m \times 100$ . The practical approach is therefore to pad given data with zeros. Padding followed by Fourier transformation $\bold F$ can be expressed in matrix algebra as

$\begin{displaymath} {\rm Program} \eq \bold F \ \left[ \begin{array}{c} \bold I \\ \bold 0 \end{array} \right] \end{displaymath}$

(6)

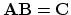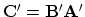According to matrix algebra, the transpose of a product, say $\bold A \bold B = \bold C$ , is the product $\bold C' = \bold B' \bold A'$ in reverse order. So the adjoint subroutine is given by

$\begin{displaymath} {\rm Program'} \eq \left[ \begin{array}{cc} \bold I & \bold 0 \end{array} \right] \ \bold F' \end{displaymath}$

(7)

Thus the adjoint subroutine truncates the data after the inverse Fourier transform. This concrete example illustrates that common sense often represents the mathematical abstraction that adjoints of products are reverse-ordered products of adjoints. It is also nice to see a formal mathematical notation for a practical necessity. Making an approximation need not lead to collapse of all precise analysis.

Next: Nearest-neighbor coordinates Up: FAMILIAR OPERATORS Previous: Zero padding is the

2009-03-16